依据课标研教材 立足学情巧设计——《等腰三角形》教学反思（杨艳丽）

等腰三角形的性质是青岛版八年级上册第二章第六节第一课时的内容，它被安排在轴对称和全等三角形的判定之后。本节课主要的学习内容是“轴对称”“等边对等角”“三线合一”三个性质，这节课的内容既是前面知识的深化和应用，也是今后学习等边三角形的基础知识，还是今后证明角相等、线段相等、两直线相互垂直的依据，因此这节课具有承上启下的作用。

八年级的学生已经初步具备了一定的抽象思维能力，一定的独立思考、实践操作、合作探究、归纳概括的能力，能够进行简单的推理论证，同时也掌握了一般三角形和轴对称的知识。

《数学课程标准》指出：数学的抽象结论，应以观察、实验为前提，几何数学应该把试验方法与逻辑分析集合起来。

基于以上认识和学情分析，在备课时我认真地研究课程标准，反复阅读教材，最后确定了本节课的三个学习目标：

1、探究并掌握等腰三角形的性质

2、运用性质解决角或线段的计算、证明问题

3、体会转化、分类讨论等数学思想

为了能够更好的完成教学目标，我决定从学生的已有知识储备和生活经验出发进行教学设计，坚持学生主体，教师主导，师生互动，生生互动的理念，致力于激活学生已有知识来调动学生的兴趣和积极性，充分挖掘学生潜力，着意指导学生亲自动手实验，亲身经历观察，猜想，验证，归纳。

复盘整节课，我觉得有以下几个方面做的较为成功：

1、对教材内容的大胆调整。

教材通过作图、对折、思考等活动引导发现三个性质。对此，我设计了“剪一剪、折一折、猜一猜、证一证、归一归”五个教学活动，旨在帮助学生由观察比较到猜想归纳，由猜想归纳到推理论证;由个别形象到一般抽象;由感性认识到理性认识，使学生的思维由形象直观到抽象的逻辑推理，层层展开，步步深入，揭开对“等边对等角”、“三线合一”正确理解的疑难。

这里调整最大的是课本上没有对性质2、3进行严格的逻辑推理，因为数学是“求真”的，所以对性质的探索上我大胆地增加了“证一证”这一教学环节，本环节通过学生小组合作交流，分享不同作辅助线的方法，拓宽了学生思路，发展了学生的思维能力；同时这种作法不仅使学生“感到自然，好接受”，更重要是体现数学性质定理的探究过程“实验-猜想-证明-归纳”，为以后的数学性质定理的学习建好模型。同时，为了降低“三线合一”包含的3个含义的难度，我以填空的形式引导学生一起给出1种情况的规范几何语言，生再仿写另2种情况。从课堂教学效果来看，这些调整很有效果很成功。

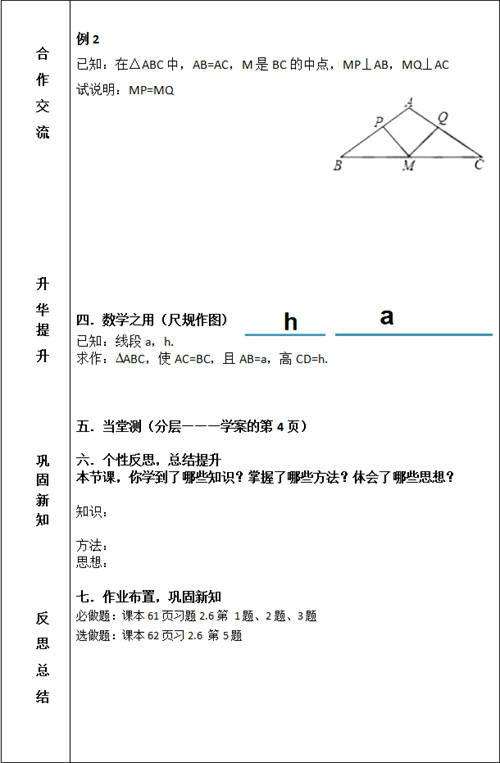
2. 对例题的精心选择

本节课，在例题的选择上既源于教材又优于教材。课本例1是对“等边对等角”的应用，我改为以“刮刮乐”的3个有梯度的填空题形式呈现，扩大例题的辐射面，实现了一题多变，无疑提高了学生的解题能力和思维严密性。课本上对“三线合一”没有对应的例题，我设计的例1、例2都采用让学生先独立思考，再小组合作交流，并让学生板演讲解的形式，给学生提供交流的空间和展示的空间，让学生教学生，增强学生的自信心。通过例题的一题多解及层层变式，学生对“三线合一”理解又深了一步， 拓宽了学生的思维空间，有助于学生打破思维定势（证明两条线段相等就去证明三角形全等的固有模式），而又形成新的思维定势（利用等腰三角形的“三线合一”证明线段相等、角相等、线段垂直的新方法）。例1例2的设置提供了学生自主探索几何学习的舞台，营造了思维驰骋的空间，有利于培养学生思维的变通性和灵活性，较好地对课本知识进行了迁移应用，较为成功。

刮刮乐：

1.已知等腰三角形的底角为40°，则另两个角的度数为_________

2.已知：△ABC中，AC=BC，∠A=100°，则∠B=____，∠C=____.

3.等腰三角形中一个角为40°，则另两个角分别等于_________

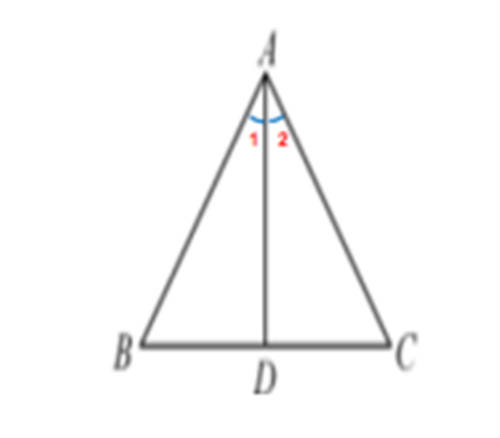
学案例1变式：如图，在△ABC中，AB=AC.

(1)若∠1=∠2，BD=3， 则BC=___.

(2)若AD⊥BC，∠1=20°,则∠BAC=___.

(3)若BD=CD，则AD与BC的位置关系是_____.

3. 对课本知识从数学思想、数学方法上渗透升华。

“解题千万遍，解后抛九霄”，难以达到提高解题能力、发展思维的目的。善于作解题后的方法的归纳、数学思想的提炼、技巧的揣摩是数学学会的根本。本节课，对性质的证明中渗透“转化”思想；对“等边对等角”的应用中渗透“分类讨论”思想；在仿写“三线合一”的几何语言中渗透“类比”的思想；在限时测试求角度中渗透“方程思想”。性质的证明及例2中等腰三角形常见的辅助线的作法引导，这些思想和方法的渗透，都有助于学生对所学知识的理解，同时还培养学生的数学能力和数学品质，促进学生核心素养的发展，从而内化成自己的一种特殊素养！

4. 对作业的分层设计

课堂检测是课堂教学效果评价最为直接和有效的手段，同时学生的基础也具有不平衡性，为此，在作业的设计上我采用了分层设置作业的形式，以满足不同层次学生的个性化需求，收到了很好的效果。

本节课基于“数学来源于生活又服务于生活”理念的教学设计让学生体会的淋漓尽致。从“生活中美丽等腰三角形建筑的图片”的情景设置导入新课，到让学生动手“剪一剪”“折一折”，到最后“数学之用——利用‘三线合一’测试水平面是否水平”结束。通过演示自制教具，激发学生的探索能力、热爱数学的激情、培养学生科学的研究方法、实事求是的做事态度，这些都是值得坚持的地方。

当然，本节课也诸多的遗憾和不足值得反思和改进：

1. 对学情把握不够精准。

这一点在备课时处理的不够精细和精准，也导致在课堂教学中对性质的证明探索分享环节用时长；巡视各小组的讨论时，老师没有控制好，导致学生分享时用时过长；对学生讨论的“有效性”没有充分的把握，教师应调控好讨论的“收”、“放”、“度”。

2. 对教学环节取舍把握不当。

为了提升课堂效果，45分钟的课堂设计不可能面面俱到，必须大胆做出取舍。本节课，“剪一剪”对学活动改为剪好的不同形状的等腰三角形提前发给学生可节省时间；本节是等腰三角形的第一课时，对等腰三角形常作的辅助线很生疏、对“三线合一”应用不熟练很符合学情，例2可以舍去。例1让学生充分的展示，并落实好规范的解题步骤，对例1的变式作为开放性题目，自选一个写出规范的几何语言，同位再对批，这样不仅降低了难度，节省时间，同时对“三线合一”理解的进一步再夯实及几何语言的再规范，最重要的是给学生创造出碰撞思维火花的“契机”与“舞台”，学生应该更乐于参与。

3. 对“数学生活之用”这一环节处理过于仓促。

如果每个组有一套提前准备好的工具，再小组讨论如何测试课桌面是否水平，最后小组演示分享，这样更能体现“数学服务于生活”、“学生主宰课堂”。

4. 对于学生的评价过于单一。

评价应该及时多样，这样才能充分调动学生的学习激情，让学生更投入课堂。分层教学环节只体现在限时测试中或作业的布置中，太表面性，如何设计在整节课中实施分层教学是今后应深思的问题，也是以后教学值得研究的课题。同时小组合作的形式太局限，缺乏小组之间的交流。

总之，课堂教学永远都是一门缺憾的艺术，教学一途，吹沙拾金，我们只有在不断的研究课标、教材，研究学情、教法上不断努力；在教学实践中不断反思，最终才能千淘万漉，吹尽黄沙始到金。

附：教学设计

2.6等腰三角形（1）（个性超市）——当堂测 （根据自身情况，任选一层） 姓名——班级——

A层【基础固本】（共15分）

1（5分）在等腰△ABC中，AB＝AC，∠B＝50°，则∠A的大小为________．

2. （5分）等腰三角形的两条边长分别为1和2，则这个三角形的周长是 （ ）

A. 4 B. 5 C.4或5 D.不能确定

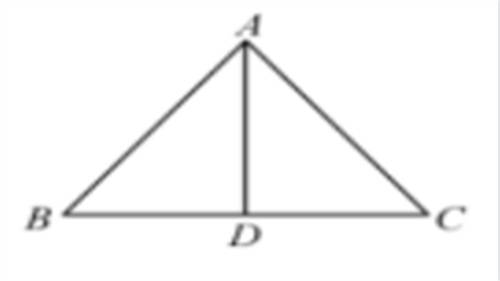
3.（5分）在△ABC中，AB=AC，AD⊥BC于点D，若AB=6，CD=4，则△ABC的周长为_______

B层【中档淘金】（共20分）

1（5分）等腰三角形的一个内角为70°，则另外两个内角的度数分别是 __________________

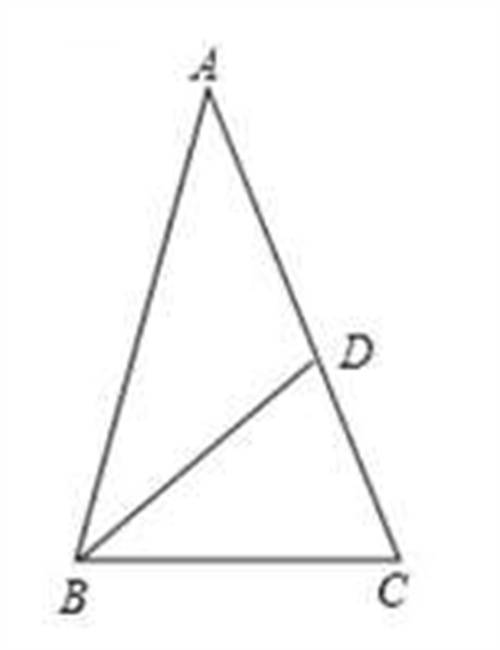
2.（15分）在△ABC中，AB=AC, 点D在AC上， 且BD=CB=AD，则∠C=_____

试说明理由.

C层【拔高培优】（20分）

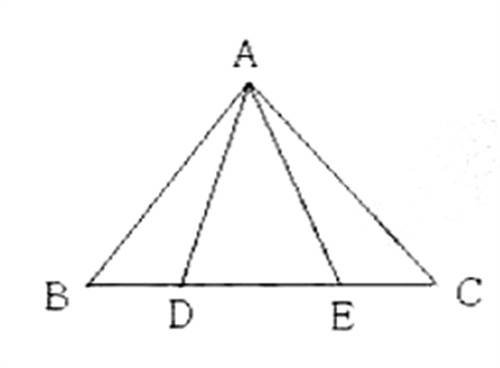
（挑战中考）已知：点D、E在△ABC的边BC上，AB=AC，AD=AE

求证：BD=CE(你有几种证法？一种证法20分）

作者：杨艳丽